There’s a lot of pages and pictures on social media, presenting polyamorous people in so-called triads or throuples, meaning that three people are in a relationship with each other. (As opposed to a “vee”, where two people are in a relationship with the “hinge”).
Now many people are in one relationship that makes them happy, but trying polyamory might endanger that. How to manage time and other resources without possibly endangering the existing relationship? The solution: “Unicorn Hunting”. This term usually describes a couple, consisting of a heterosexual cis man and a bi/pansexual cis woman, looking for “a third”, most likely another bi/pansexual. But you can also use the term generally to describe a couple looking for a third (which is what I will be doing here).
There’s already a lot of articles on how many Unicorn Hunters are approaching this in an unethical way, or well-meaning couples that aren’t aware of their couple’s privileges (Check out unicorns-r-us.com!) and the Unicorn, a polyamorous, bisexual person that likes both partners, is named after its rarity. How rare it might be and what can you do about it? Let’s run some numbers.
Disclaimer: Those probabilities here are assumed and might vary between people. You can fill in your own probabilities, but I’m pretty sure your conclusion won’t differ. I’ll try to use optimistic numbers for this scenario.
Let’s say, the chance for you to find a partner, if you ask only people of a gender that match your sexuality and aren’t clearly monogamous, is one in a hundred (x) people. We get a probability of 1%. Isn’t much but I can find a lot of people on dating apps, can’t I? Our formula for now is:
1 / x = 1 / 100 = 1%

Now this partner has also to be a suitable partner for my partner. But let’s be more optimistic here, since they like me the chance of them also liking my partner and vice versa could be one in ten (y). Now we’re at:
1 / xy = 1 / 1 000 = 0.1%
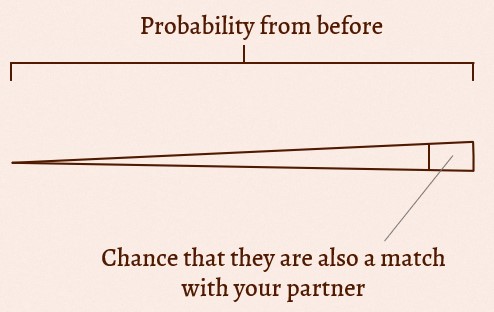
But also, now we must take into account that there’s a least one non-heterosexual relationship happening. Because it seems to be more likely to find queer people in the polyamorous community than outside of it, I’ll take the biggest number I can find it a study and double it. Which means, the chance of the Unicorn to have a “fitting sexuality” is one in ten again (z). Of course, this might be different if a homosexual couple is looking for the opposing gender. Our chances are now:
1 / xyz = 1 / 10 000 = 0.01%
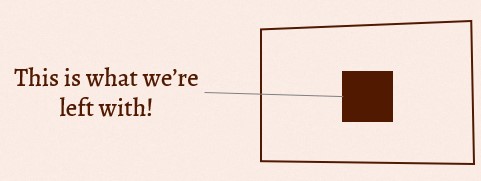
And now there’s one more thing to consider. A relationship between three people consists of four relationships, not three. Besides three individual couples, you have to work as a triad. After considering all the difficulties like proper time management, couple’s privilege and so on, opposed to that we have three people that love each other and want to make it work. Taking into account how different people might be and how little data there is, I’ll assume the chance of this working out to be one in two (w). Our final chance to find a unicorn is:
1 / wxyz = 1 / 20 000 = 0.005%
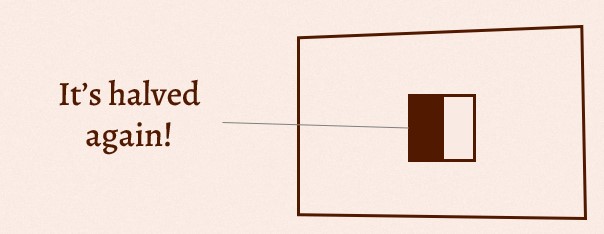
Imagine contacting 20 000 people. That’s a lot of people and you might still be unsuccessful. So what can you do to improve your chance? The PolyPirates recommendation is: Date separately! But how will this help you if it’s the exact opposite of what you want? This works because those vexing variables go away after their events happen. Let’s say you find a new partner that likes you back, and they just happen to have a suitable sexuality for a triad, the chance of that (1 / xz) might be one 1 in a 1000, but considering that this is also every person you just swipe left, it’s much more feasible. It’s like finding a shiny Pokémon, it might take a lot of grinding, but it also just happens along the way.
But will your new partner and your old partner also get in a relationship? We are left with a one-in-twenty chance (1 / wy = 5%), which sounds rather small since we got only “one try” per partner. But come on, look at you! Even if it doesn’t work out, you’re in two loving relationships, so what are you complaining about?

